Remember that frustrating time in geometry class when you were struggling to grasp the properties of parallelograms? You were tasked with completing a worksheet, but the answer key seemed as elusive as a unicorn. Well, fret no more! In this comprehensive guide, we’ll dive deep into the world of parallelograms, exploring their defining characteristics and tackling those pesky worksheet questions with confidence. Consider this your ultimate guide to mastering the properties of parallelograms and conquering any worksheet that comes your way.
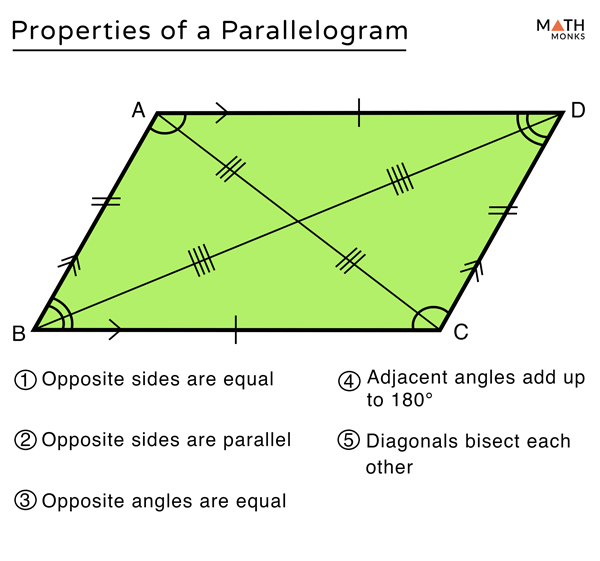
Image: answerschooldaryl.z13.web.core.windows.net
From understanding the basic definition of a parallelogram to applying its unique properties, we’ll break down each concept step-by-step. We’ll even go through some practice problems from a typical “properties of parallelograms worksheet” to help solidify your understanding. By the end, you’ll have a firm grasp of this crucial geometric shape and be able to confidently solve any related problem.
Understanding the Fundamentals of Parallelograms
A parallelogram is a four-sided polygon, or quadrilateral, where both pairs of opposite sides are parallel. This simple definition opens the door to a world of unique properties that make parallelograms stand out among other quadrilaterals.
One of the most important properties of parallelograms is that opposite sides are equal in length. This means that if you have a parallelogram with side lengths AB and CD, then AB is equal to CD, and BC is equal to AD. This property makes it easier to calculate the perimeter of a parallelogram as you simply need to find the lengths of two adjacent sides and multiply by two.
Beyond Parallel Sides: Exploring the Key Properties of Parallelograms
While the parallel sides define a parallelogram, there’s more to discover! Let’s explore a few key properties:
Opposite Angles are Equal
Let’s say our parallelogram has angles A, B, C, and D. In a parallelogram, angle A is equal to angle C, and angle B is equal to angle D. This property is a direct consequence of the parallel sides, as the angles formed by the intersection of a transversal line with parallel lines are equal.

Image: worksheets.decoomo.com
Consecutive Angles are Supplementary
Consecutive angles are those that share a side. For example, in our parallelogram, angles A and B, or angles B and C, are consecutive. These angles add up to 180 degrees. This makes sense because if we consider the parallel sides again, consecutive angles formed by the intersection of the transversal with the parallel sides are supplementary.
Diagonals Bisect Each Other
The diagonals of a parallelogram are the lines connecting opposite vertices. In our parallelogram, the diagonals would be AC and BD. These diagonals intersect at a point called the midpoint, where each diagonal is bisected, meaning it’s cut into two equal parts. This property is useful for determining the center of the parallelogram and finding the lengths of the diagonals.
Area Formula
The area of a parallelogram is calculated by multiplying the base length by the corresponding height. The base can be any side of the parallelogram, and the height is the perpendicular distance from the base to the opposite side. This makes it simpler to calculate the area compared to other quadrilaterals where you might have to break down the shape into simpler figures.
Mastering the Properties of Parallelograms: Real-World Examples
Parallelograms are found everywhere, from the windows in your house to the diamond pattern on a basketball court. Understanding their properties allows us to design and construct structures that are both aesthetically pleasing and structurally sound.
For example, architects use parallelograms to design strong and stable buildings. By understanding the properties of parallelograms, they can make sure the walls and roof are properly supported and will not buckle under pressure. In carpentry, parallelograms are used to create sturdy frames for furniture, doors, and windows. The opposite sides of a parallelogram ensure that the frame is symmetrical and will not warp over time. Even the simple act of tiling a floor or decorating a room with wallpaper often uses parallelograms to create patterns and visual interest.
Tackling the “Properties of Parallelograms Worksheet”
Let’s put your knowledge to the test with a sample problem from a typical “properties of parallelograms worksheet”:
**Problem:** ABCD is a parallelogram, and angle A is equal to 60 degrees. Find the measure of angle C.
**Solution:** We know that opposite angles in a parallelogram are equal. Therefore, angle C is also equal to 60 degrees.
This is just one example of the many problems that you might encounter on a “properties of parallelograms worksheet”. By understanding the properties of parallelograms, you can solve such problems with ease. It’s important to remember that these problems are designed to help you understand the concepts and to apply them in different contexts.
Tips and Expert Advice for Mastering Parallelograms
Here are a few key tips to help you excel in understanding and working with parallelograms:
- Visualize the Concepts: Draw diagrams and label the sides, angles, and diagonals to clearly represent the problem. This will help you visualize the properties and relationships within the parallelogram.
- Practice Makes Perfect: Work through various problems on worksheets and online resources to solidify your understanding. Start with basic problems and gradually work your way up to more complex ones.
- Connect with Real-World Applications: Look for examples of parallelograms in your everyday life. This will help you see how the properties you are learning are applied in practical situations.
- Don’t Give Up: Geometry can be challenging, but don’t get discouraged if you don’t understand something right away. Take your time, ask for help when needed, and keep practicing. You’ll get there!
Frequently Asked Questions (FAQ)
Q: What are some common mistakes students make when working with parallelograms?
A: Common mistakes include confusing the properties of parallelograms with those of other quadrilaterals like rectangles or squares. It’s also easy to misinterpret the angles and sides of a parallelogram, especially when working with diagrams that are not drawn to scale.
Q: Are all quadrilaterals parallelograms?
A: No, not all quadrilaterals are parallelograms. A parallelogram must have two pairs of parallel sides. There are other types of quadrilaterals, such as trapezoids, where only one pair of sides is parallel.
Q: What are some resources available for further exploration of parallelograms?
A: There are a wealth of resources available for those interested in delving deeper into the world of parallelograms. Online websites, textbooks, and educational videos offer comprehensive information and practice problems. You can also explore interactive geometry software that allows you to manipulate parallelograms and visualize their properties in real-time.
Properties Of Parallelograms Worksheet Answer Key
Conclusion
Understanding the properties of parallelograms unlocks a whole new level of understanding in geometry. From solving worksheet problems to appreciating the applications in the real world, mastering this shape opens doors to deeper insights and problem-solving skills. Remember to apply the tips we covered, practice regularly, and don’t hesitate to seek help along the way. Are you ready to conquer any “properties of parallelograms worksheet” that comes your way?
Let me know if you have any more questions about parallelograms! I’m always here to help you master this fascinating geometric shape.






